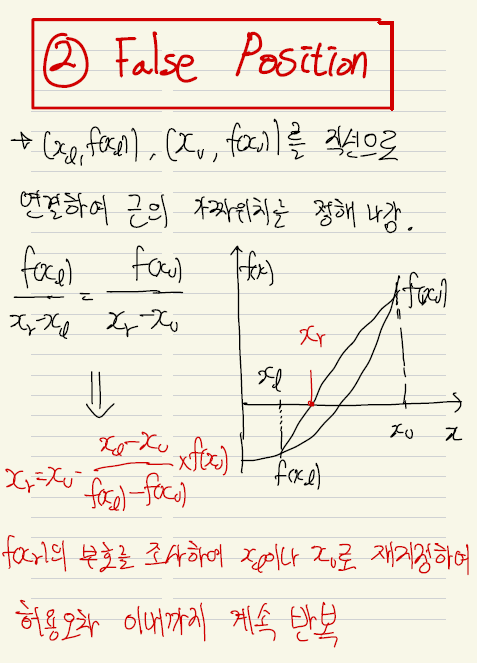
저번에는 Buck converter에 대한 내용을 봤는데, 오늘은 Boost converter에 대해서 알아보겠습니다.
(본 자료는 경북대학교 교수님의 자료를 바탕으로 만든 내용입니다)

Boost converter는 Buck converter와 다르게 Step-up 컨버터라고 불리며, 승압을 해주는 컨버터 입니다. 예를 들어 일본에서 110V의 콘센트를 쓸 때, 우리가 쓰는 220V로 변환해주기 위해 꽂는 돼지코가 승압기 역할을 해준다고 보면 됩니다.
그러면 부스트 컨버터를 강하게(?)만들면 좋지 않냐고 하는데, 보통 전압이 2배가 되면 인덕터에 많은 전류가 흘러서 스위치가 점점 뜨거워지기 때문에, 보통 Conversion Ratio가 2가 되는 경우 까지만 쓴다고 합니다. 이는 아래 내용을 통해 다시 한번 더 확인할 수 있습니다.
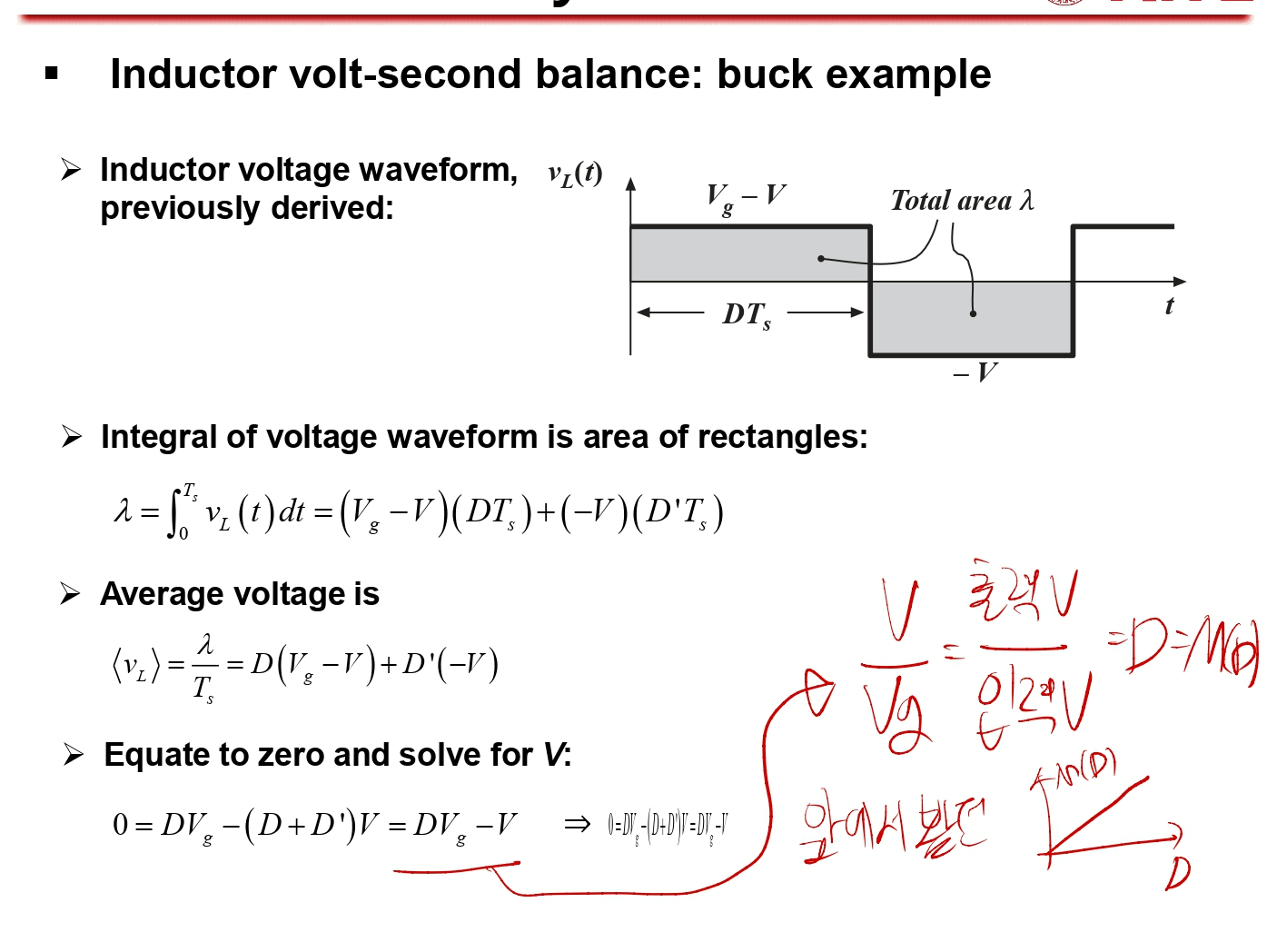
Boost Converter

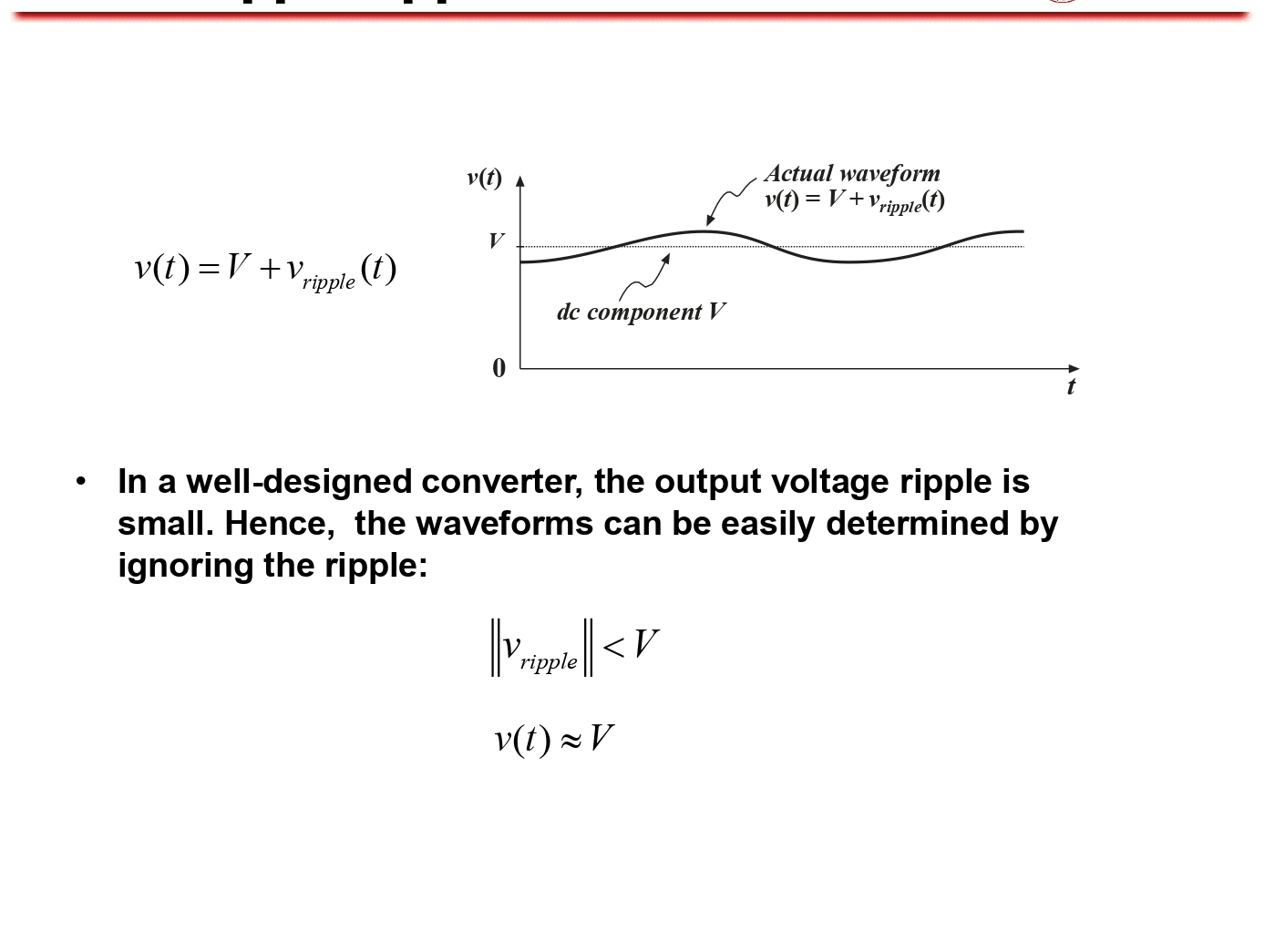
부스트 컨버터에 대한 내용을 하기에 앞서, 커패시터가 정상상태 일 때 커패시터의 전압이 일정하여, 흐르는 전류가 0이라는 것을 인지하고 갑니다.
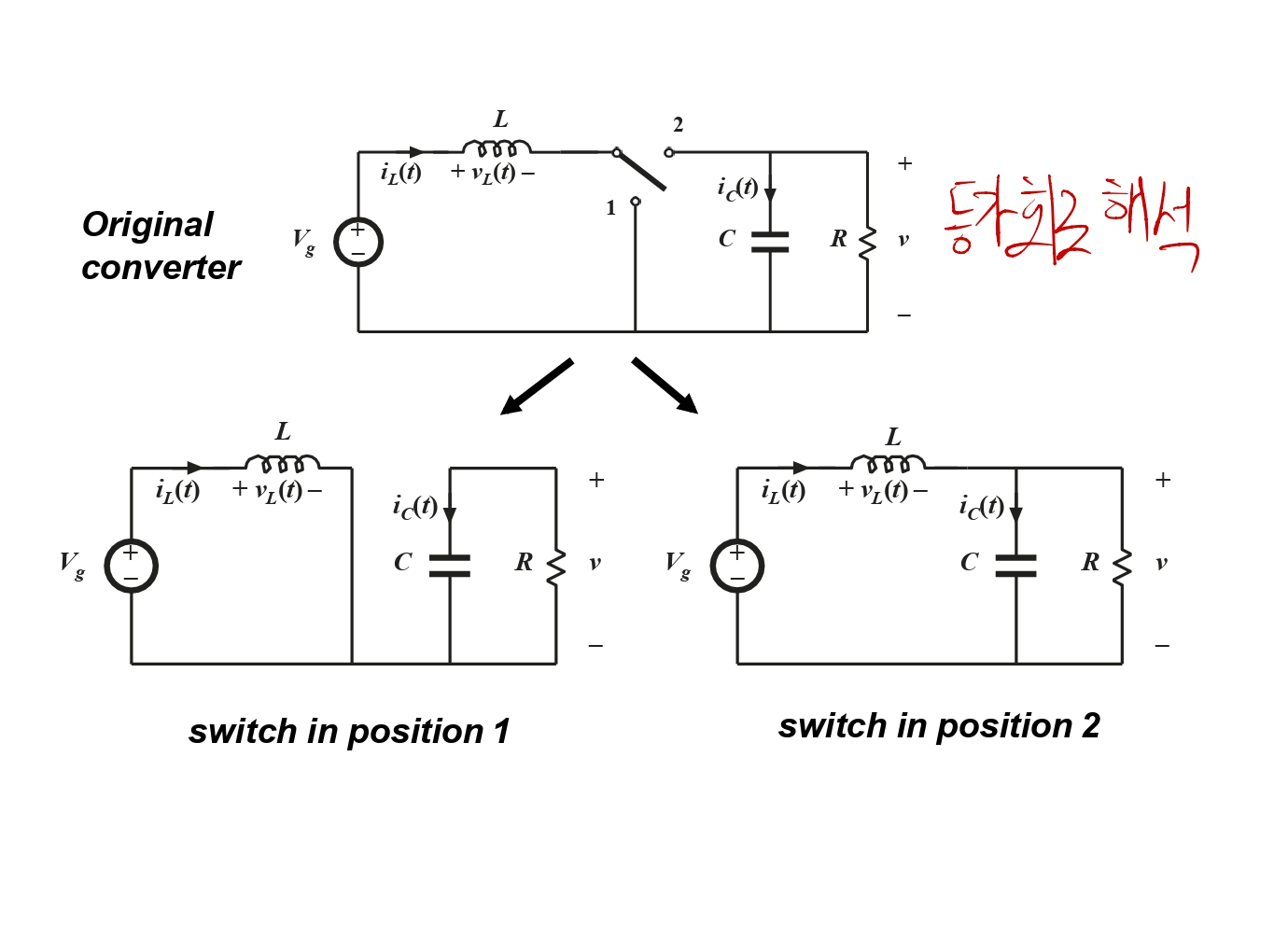
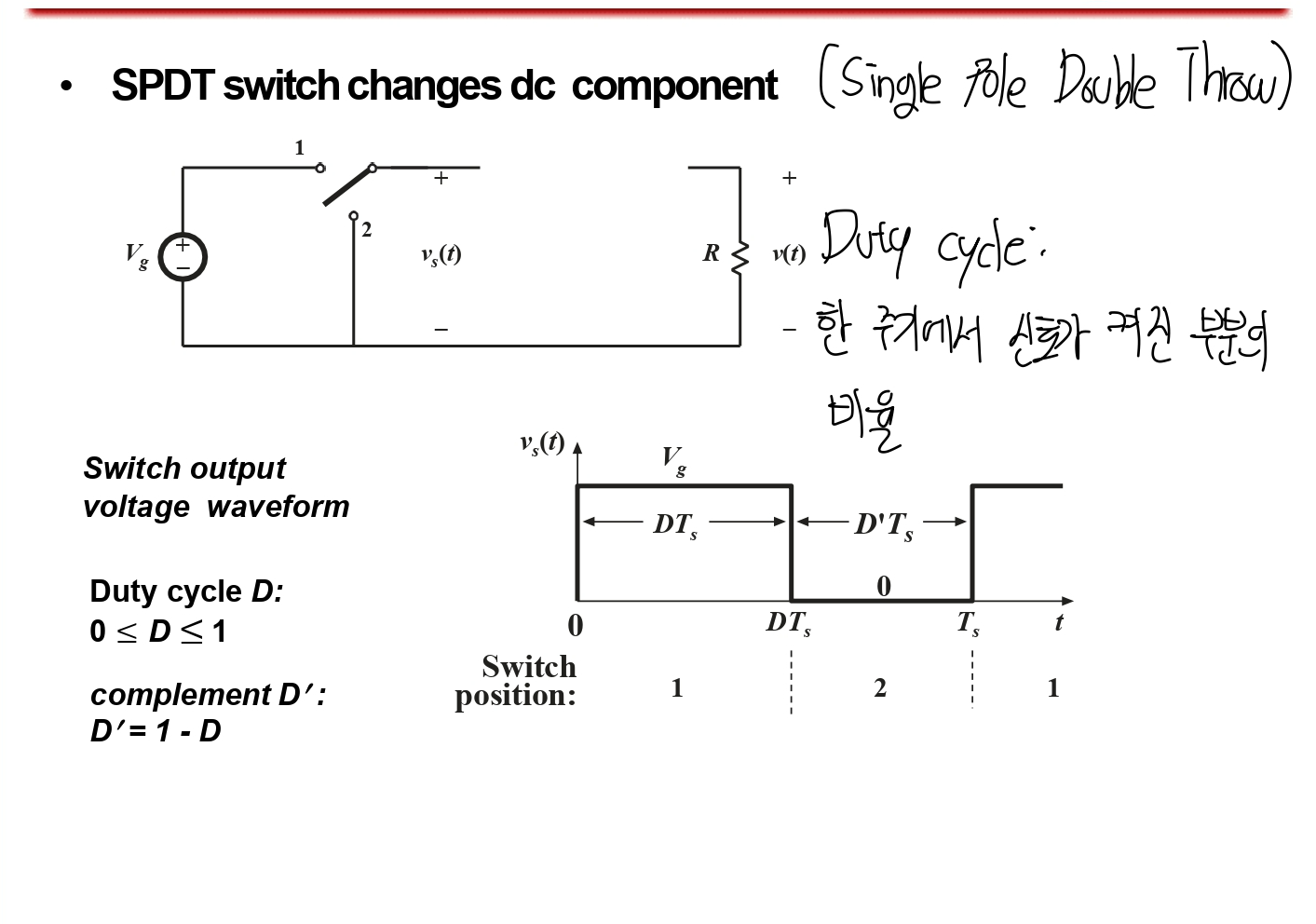
벅 컨버터와 마찬가지로, 부스트 컨버터 또한 스위치가 있기 때문에(MOSFET과 다이오드로 생각) 두 가지 케이스가 있는데, 이를 등가회로로 해석해봅니다.

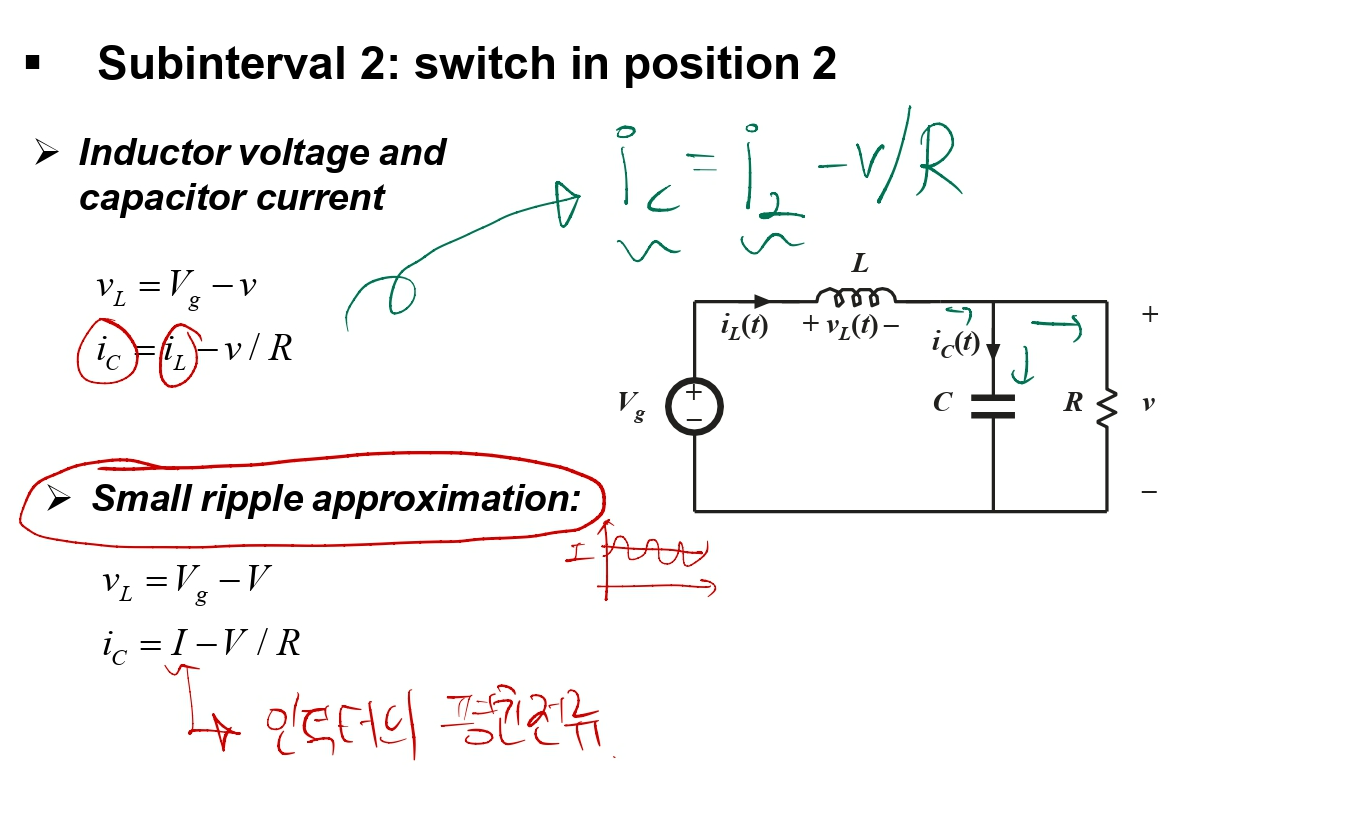
위의 식대로 가도 되지만, 출력 전류를 io로 봤을 때 io = - ic가 되는 것을 볼 수 있습니다. 왜 복잡하게 출력전류를 추가하냐고 묻는다면, 그냥 회로 공부하다 보니 출력부분에 관심이 생겨서 그렇다고 말하고 싶습니다 헤헤
두 번째 케이스를 보면, Small ripple approximation에 의해 인덕터에 흐른 전류를 I로 보고, 키르히호프의 법칙을 통해 커패시터의 흐르는 전류값을 구할 수 있습니다.
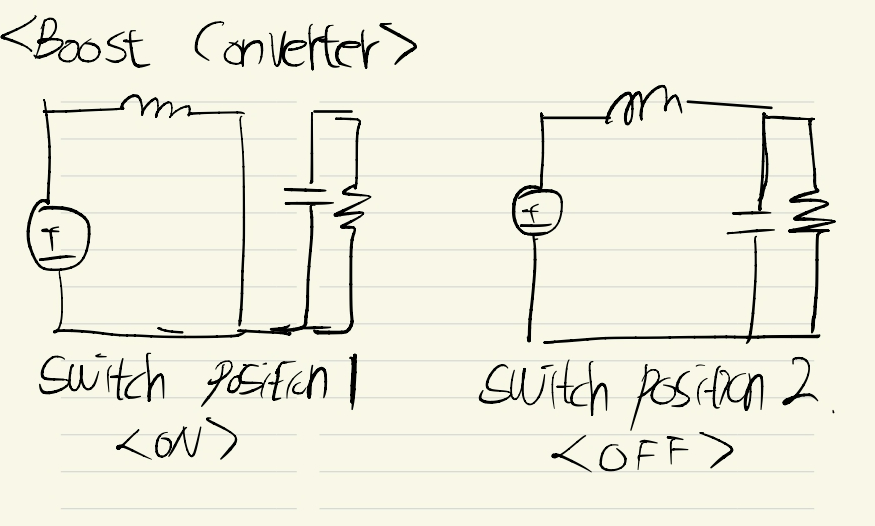
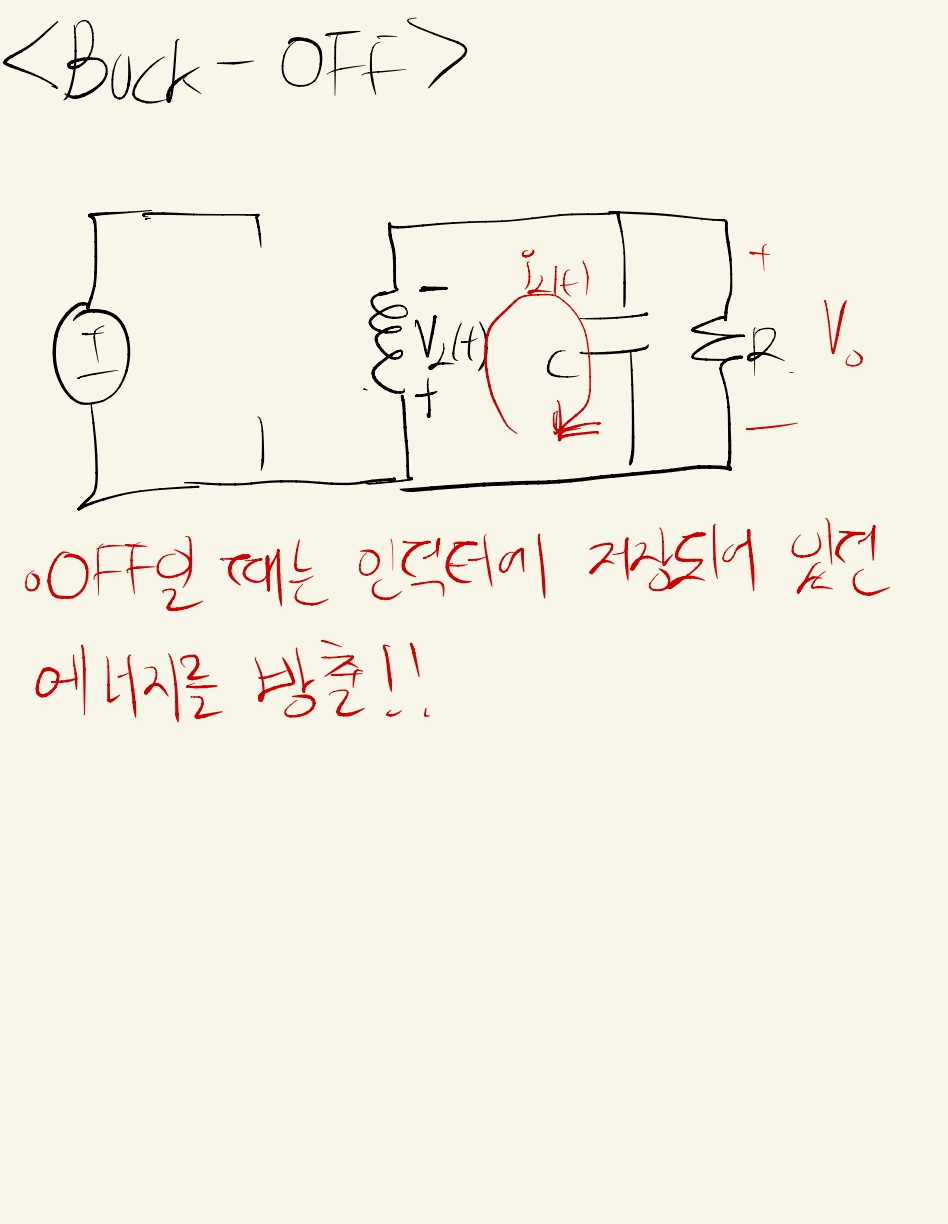
정리하면, 왼쪽은 부스트 컨버터가 ON 되었을 때, 오른쪽은 OFF되었을 때인 것을 볼 수 있습니다.
근데 부스트의 OFF부분을 보면, 마치 벅 컨버터의 ON과 유사한 걸 볼 수 있습니다.
이를 통해서 알 수 있는 것은 무엇일까...한번 고민해보려고 합니다! (반도체 잘 모르는 공학도라서 죄송합니다 ㅠ)
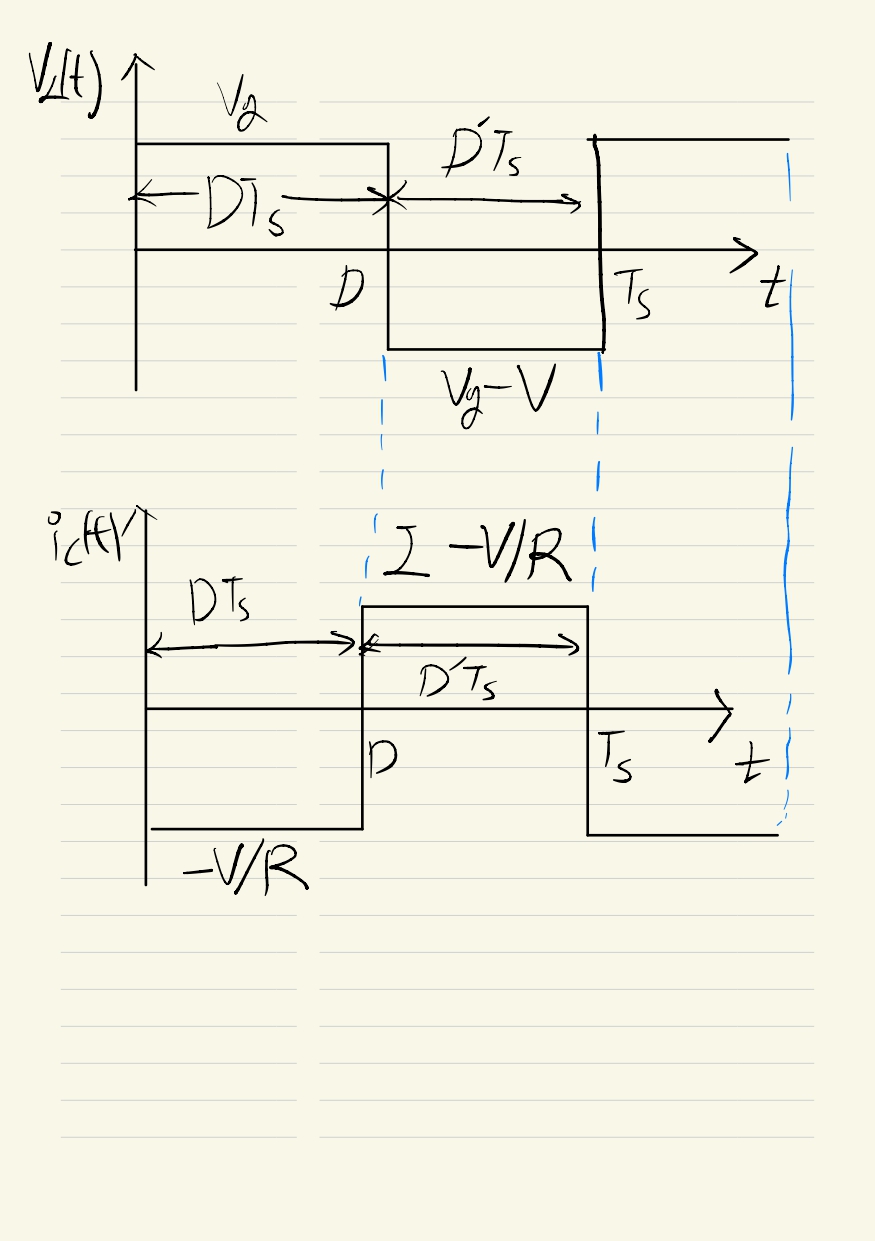
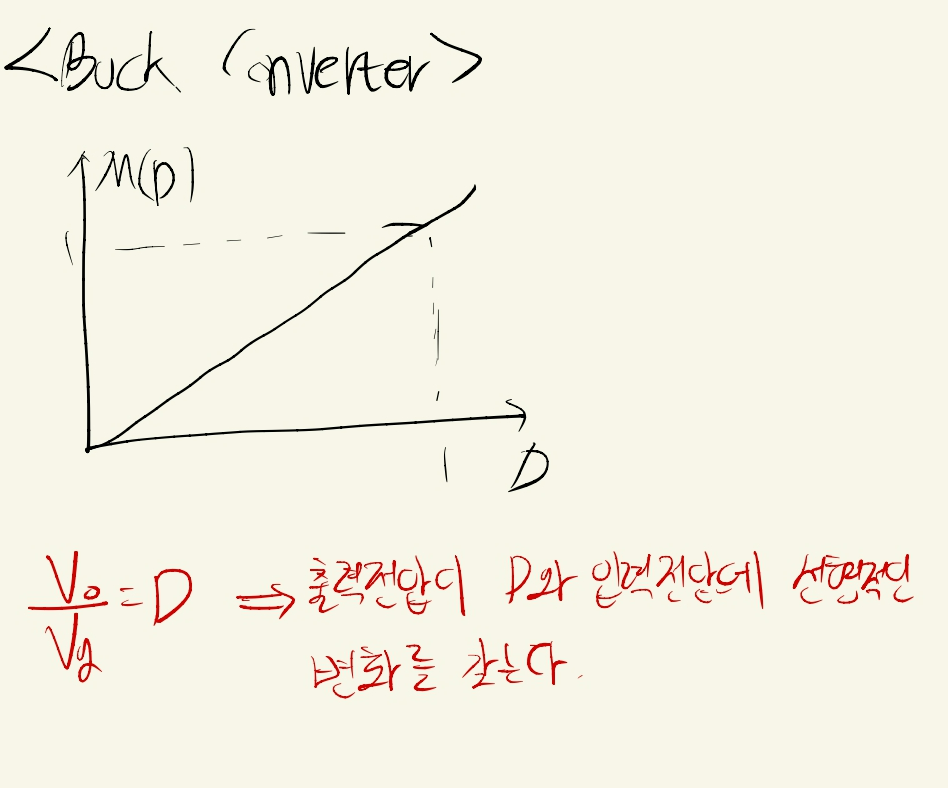
부스트 컨버터의 인덕터 전압과 커패시터 전류를 그래프로 나타냈으며, 이를 통해 Conversion Ratio M(D)를 구할 수 있습니다. 승압 컨버터이기 때문에 M(D)가 위로 가는 거라고 예상할 수 있습니다.
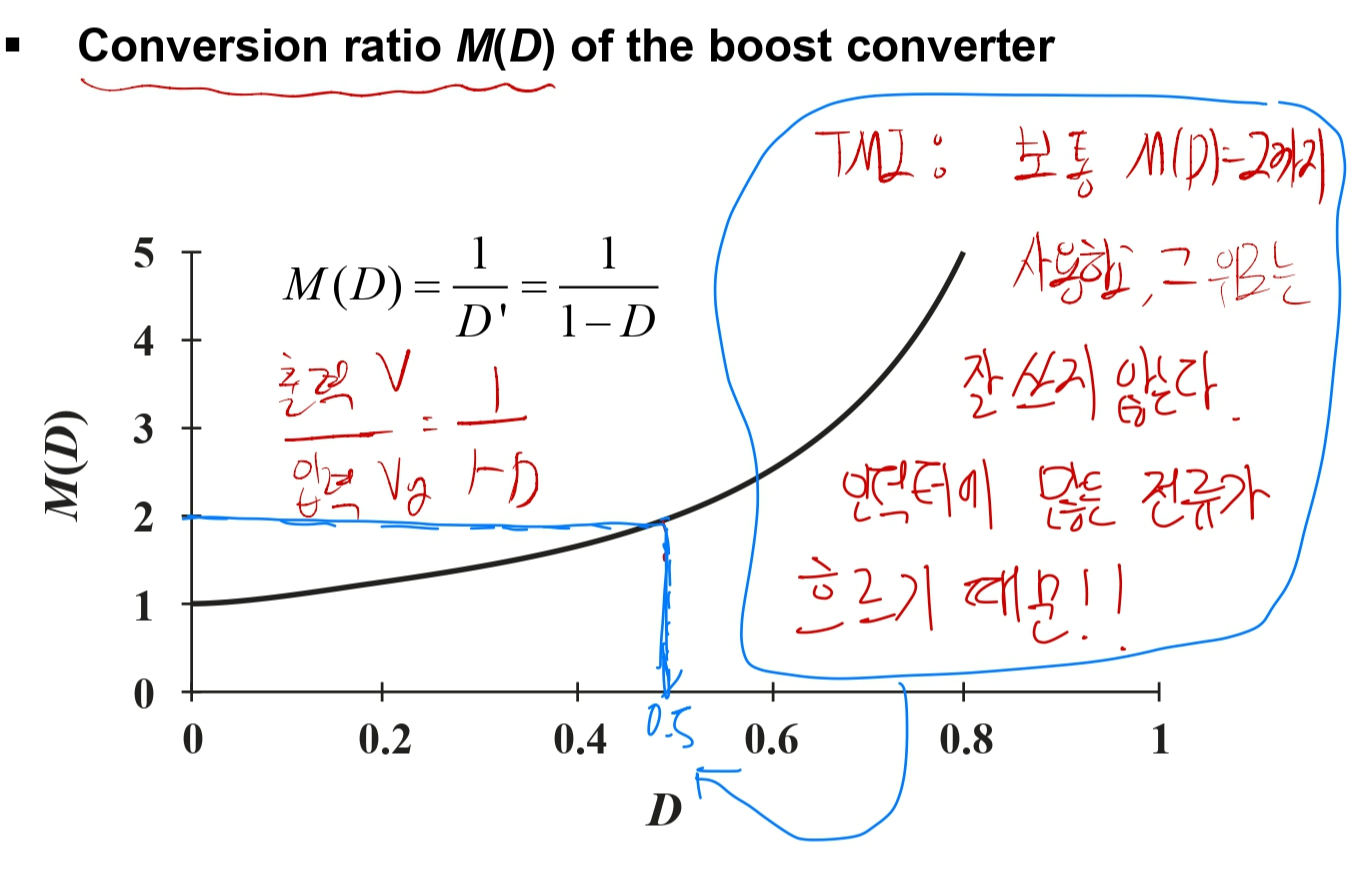
위 그림을 보면 Conversion Ratio가 승압의 형태로 나타나는 것을 볼 수 있습니다.


커패시터에 흐르는 전류를 통해서도 Conversion Ratio를 구할 수 있습니다. 이때 신기한 사실은, 출력 전류와 입력 전류의 비로 M(D)를 구할 수 있다는 겁니다.

벅 컨버터와 부스터 컨버터는 유사한 특징을 지니고 있는데, 위에 나타난 것 처럼 부스트 컨버터는 Conversion Ratio를 전류로도 나타낼 수 있다는 차이점이 있습니다.

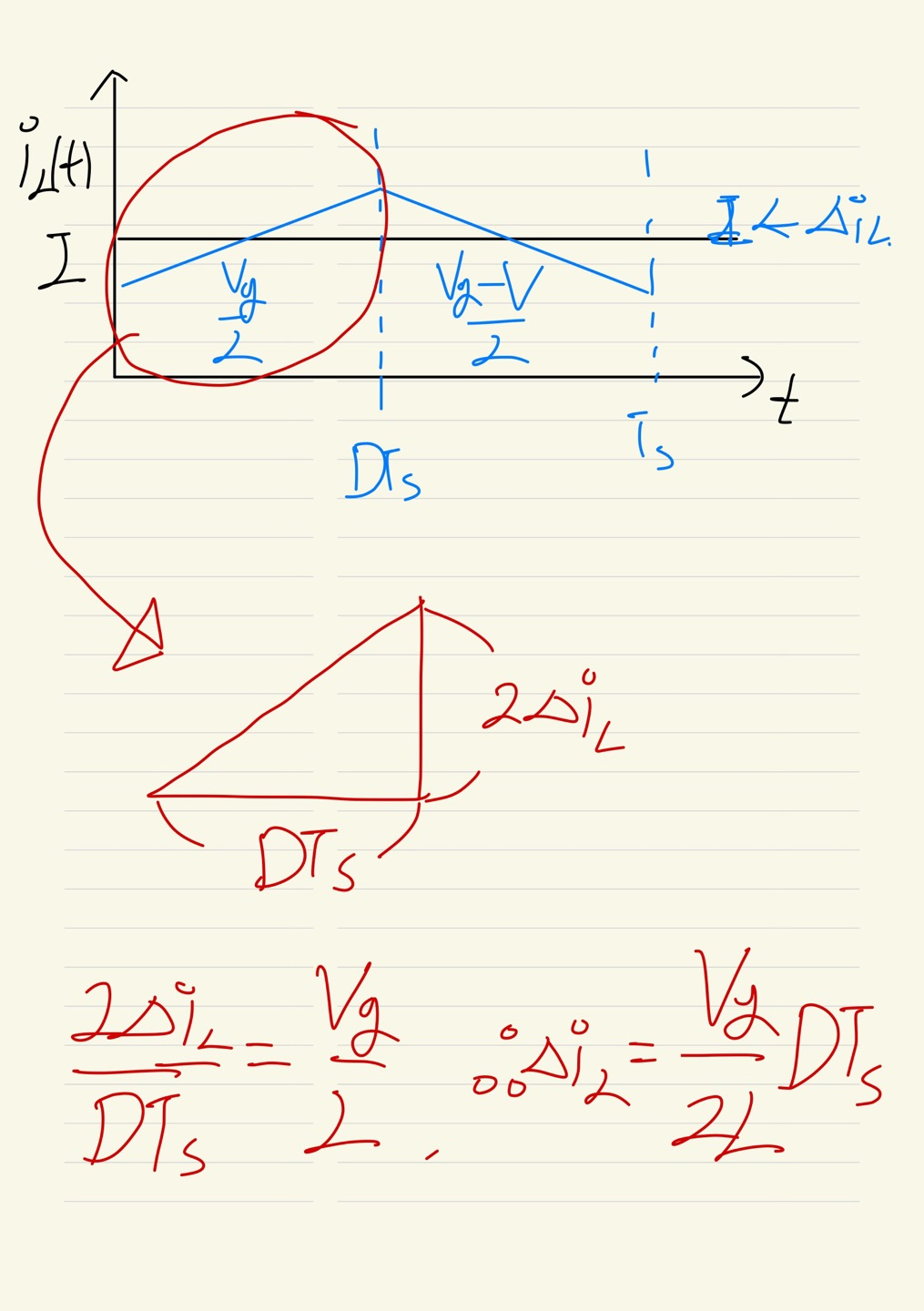
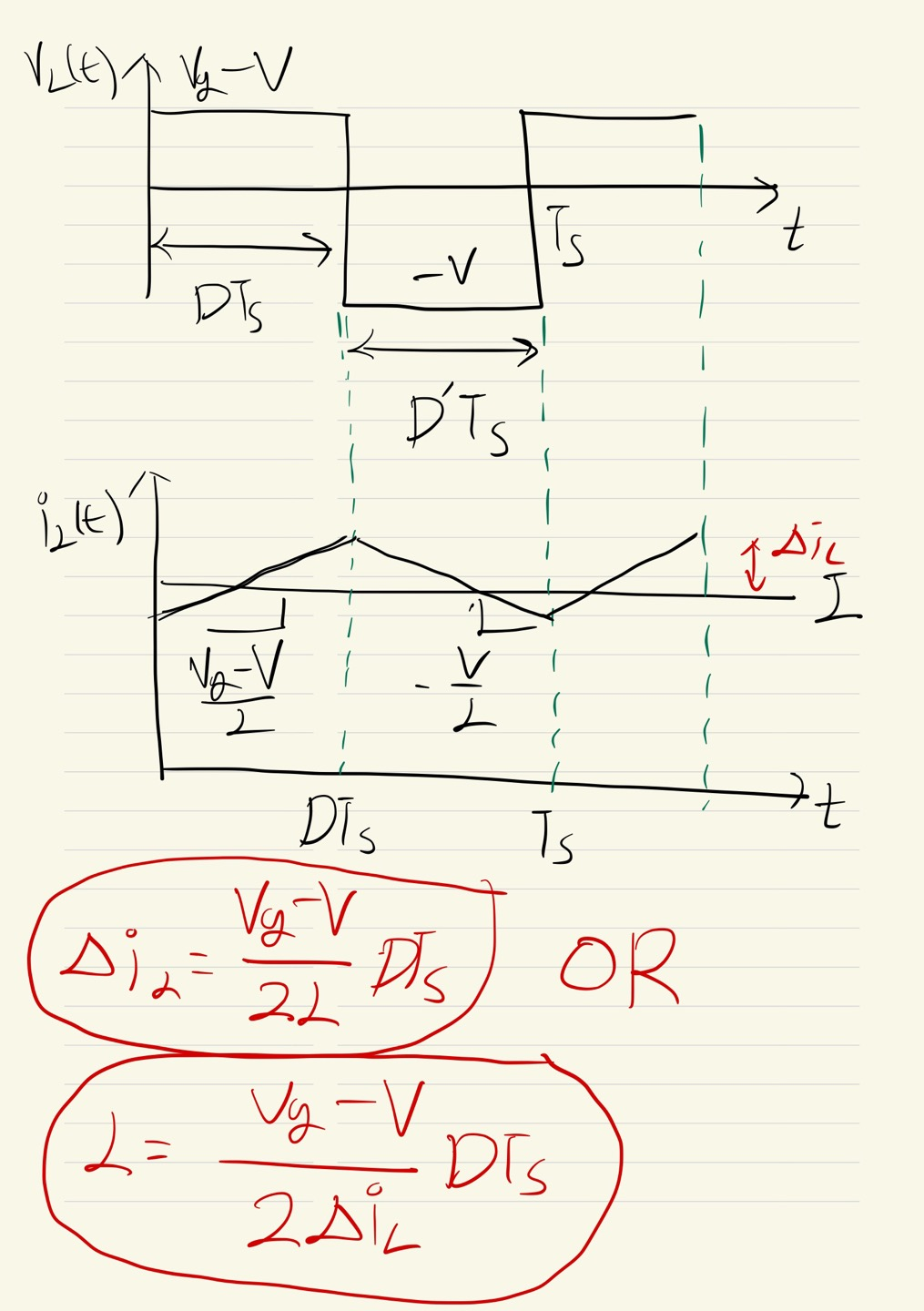
이번에는 인덕터에 흐르는 전류를 생각해봅니다. 인덕터 전압 공식을 이용하여 ON, OFF일 때를 생각하여 각각 구하고, 기울기를 통해서 iL값을 구할 수 있습니다. 즉, 리플의 크기를 조정하기 위해선 인덕턴스가 관여하는 것을 볼 수 있습니다.
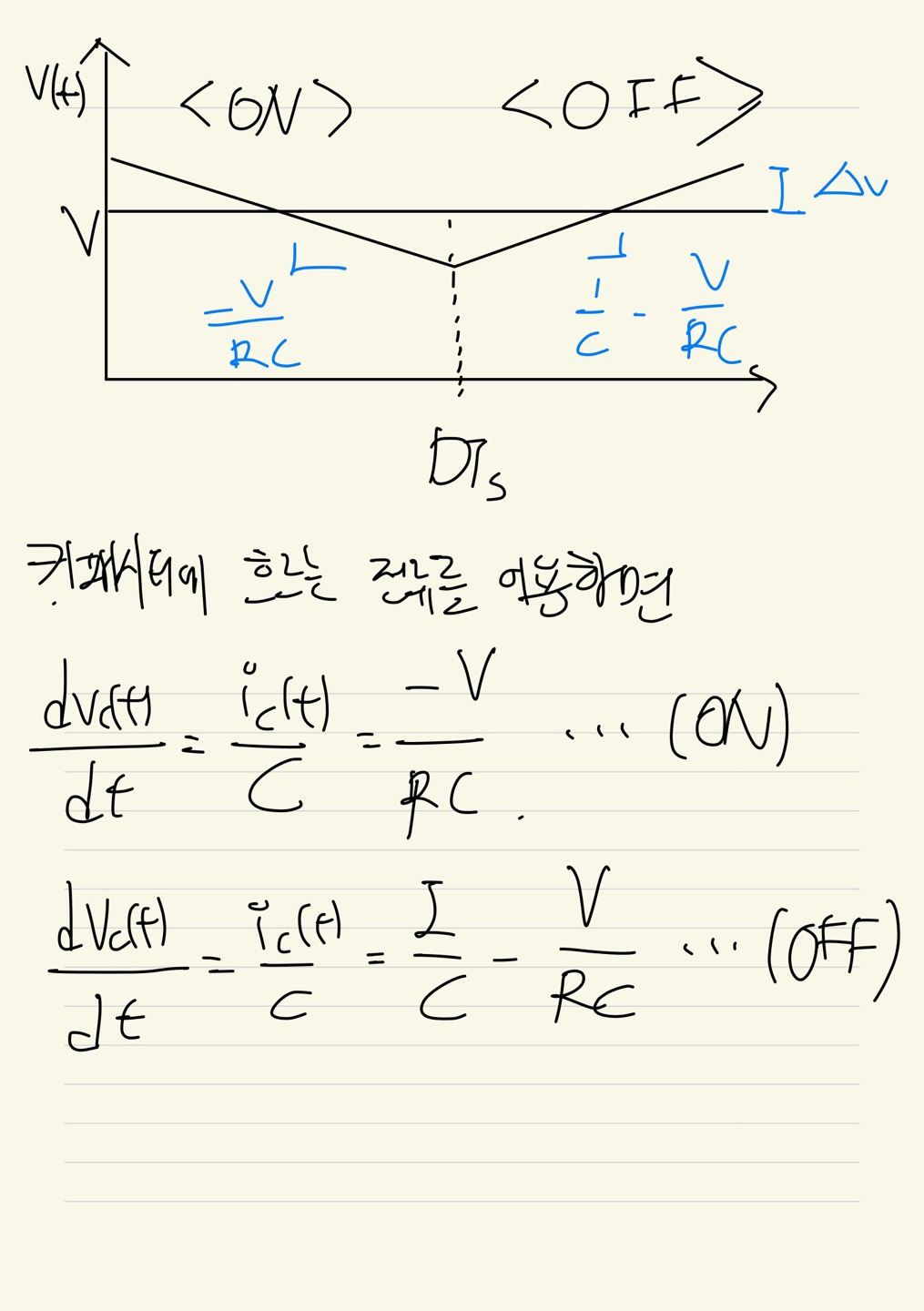
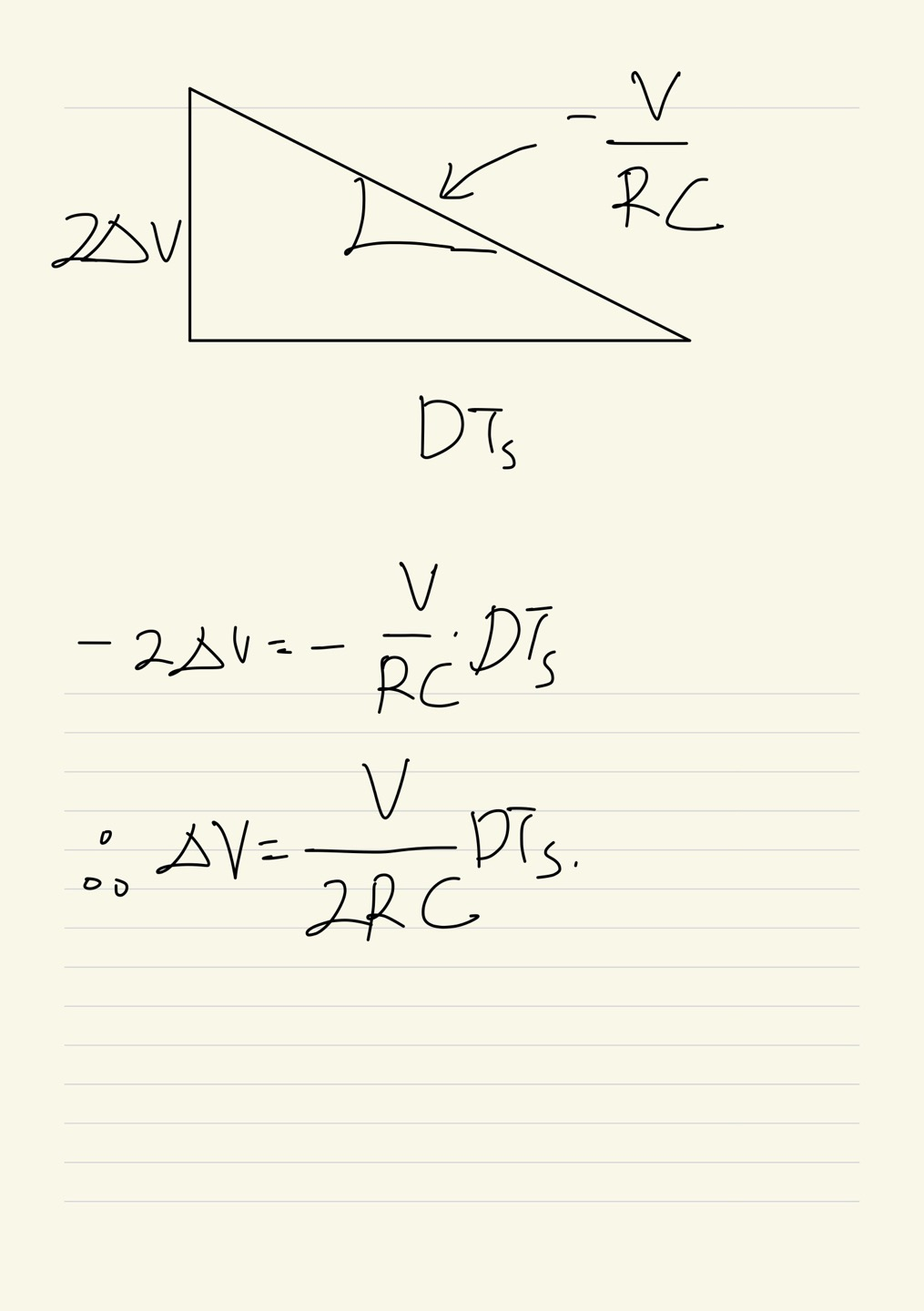
마지막으로 커패시터에 걸리는 전압을 분석할 수 있습니다.
쓰다 보니, 뭔가 중구난방이 된 부스트 컨버터 분석 글이었습니다..하하..
다음에는 축 컨버터에 대한 내용으로 돌아오겠습니다!