방황하는 20대

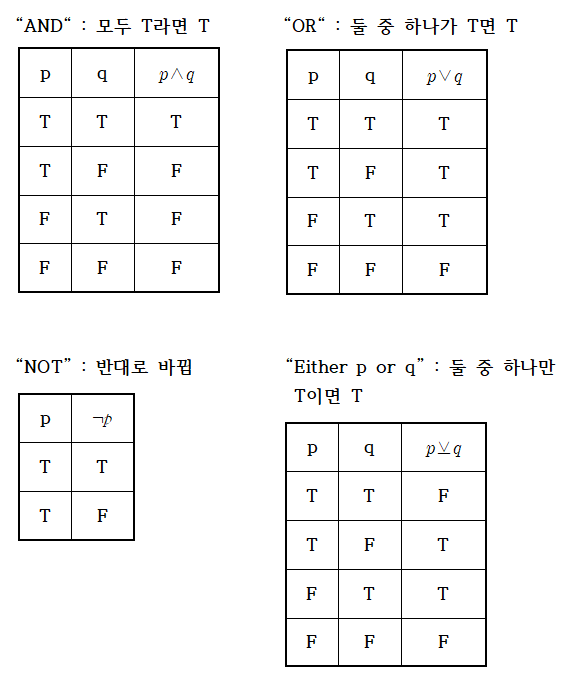
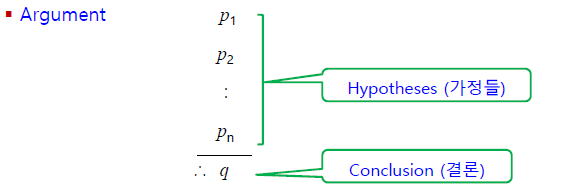
이 글은 기자분들의 뉴스를 읽고, 그 내용을 발췌하고 제 생각을 추가한 글입니다.

혹시나 틀린 내용이 있거나, 부족한 부분이 있으면 지적해주시면 감사하겠습니다!

뉴스 출처 : http://news.tf.co.kr/read/economy/1961742.htm

https://zdnet.co.kr/view/?no=20220904104031 

https://zdnet.co.kr/view/?no=20220904174309 

 삼성과 TSMC의 반도체 경쟁은 점점 고도되고 있다. 현재 두 기업 모두 3나노 공정 체제에 돌입했고, 삼성은 구글 '3세대 텐서(Tensor Gen 3)'의 수주를 받아냈고, TSMC는 놀랍게도 애플, 퀄컴, 엔비디아 등 다양한 업계의 수주를 따낸 상태이다. 단지 수주를 따낸 업체의 수만 보면 TSMC가 훨씬 많지만, 그렇다고 TSMC가 삼성보다 반도체 시장에서 우위를 차지하고 있다고 말하기는 힘들다고 본다. 왜냐하면 TSMC는 2025년에 2나노 GAA기술을 도입할 예정이지만, 삼성은 현재 2022년에 3나노 GAA기술을 도입했기 때문이다. 그리고 구글의 1세대, 2세대 텐서는 각각 5나노, 4나노의 수주였어서 삼성과 구글의 협업은 마치 공유결합처럼 단단할 것이라고 생각한다.

<여기서 3나노란, MOSFET의 채널의 길이(L)를 의미한다. 채널이 짧아질수록, 전도가 빠르고, 낮은 전력 대비 높은 효율을 나타낼 수 있다>

 그렇다면 채널의 길이가 짧아질수록, 반도체 시장이 활성화되는 걸까? 내 생각은 반은 맞고, 반은 틀리다. 무슨 의미냐면, 단순히 채널의 길이가 짧아진다는 이유 하나만 보면 정말 파격적이지만, 이를 받쳐주기 위한 다른 기술들이 필요하다. 파운드리(반도체 제조/생산) 사업이 발전하기 위해서는 설계, 화학, 에너지, 미세공정, 장비 등 다양한 분야의 기술력이 있어야 한다. 또한 파운드리는 흔히 팹(Fab : Fabrication의 줄임말, 반도체의 핵심인 실리콘웨이퍼를 만드는 것)이라고 불리며, 팹리스(Fabless: IC 설계, 판매만 하고 제조는 하지 않는 것) 와의 긴밀한 관계가 유지되어야 한다. 하나의 회사가 두 가지 팹과 팹리스를 동시에 가지고 있다면 정말 좋은데, 이것을 IDM(반도체 개발부터 설계/생산까지 모두 자체적으로 하는 업체)라고 불렀다. 놀랍게도 1980년대까지는 당연한 것으로 여겼다. 대표적으로 S전자, SK하이닉스, 텍사스 인스트루먼트 등. 그러나 최근에 들어서 높은 마케팅 능력과 높은 능력을 겸비해야 함으로 IDM업체가 파운드리나 팹리스 업체로 전환하는 사례가 늘고 있다.  

https://zdnet.co.kr/view/?no=20220904174309

 한편, 반도체 산업이 성장하고 있지만, 호황이 오기는 어렵다고 보는 전문가들도 몇몇 있다고 한다. 뉴스를 발췌해보면, 한 전문가는 "세계적으로 반도체 수요는 줄었는데 재고가 늘어 값이 떨어졌다", "미국과 중국이 기술 패권을 다투는 가운데 중국은 기술 격차를 빠르게 좁혔다"라고 보는 것이다. 메모리 반도체 가격이 3분기보다 2분기에 10%더 낮출 것이라고 보고 있다고 한다. 또한 최근에 칩4(미국의 주도 하에 미국.한국.일본.대만 국가에서 서로 협력하여 기술력을 확보하는 조약)에 대해 긍정적인 영향을 줄 것이지만 서도, 칩4에 가입한다면 결국 우리 기술력을 공유해야 하는, 희소성이 떨어진다는 생각도 나는 갖고 있다.

출처 : https://zdnet.co.kr/view/?no=20220904104031

 이렇게 부정적인 뉴스도 있는 반면에, 위와 같이 유일하게 자사 반도체의  출하량이 증가한 삼성전자의 소식도 볼 수 있었다. 뉴스의 내용을 정리해보자면

AP시장을 점유하는 대기업 중에서, 유일하게 2분기의 출하량이 증가한 건 삼성뿐이라고 할 수 있다. 이는 중,저가 스마트폰을 공략한 것의 결과로 볼 수 있다. 그러나 시장점유율은 여전히 대만이 1위라서, 아직 갈 길이 멀긴 한 것 같다!

하지만 중요한 것은, 멈추지 않고 발전하고 있다는 것이다.

이 글은 기자분들의 뉴스를 읽고, 그 내용을 발췌하고 제 생각을 추가한 글입니다.

혹시나 틀린 내용이 있거나, 부족한 부분이 있으면 지적해주시면 감사하겠습니다!

뉴스 출처 : https://www.etnews.com/20220904000052?mc=ns_001_00001

 삼성.LG 디스플레이 강국을 노리다 feat.고객경험

 삼성과 LG는 글로벌 TV 시장에서 올해 상반기 기준 각각 31.5%, 17.% 의 점유율로 1, 2위를 달리고 있다. 선두 업체가 나란히 '스크린 고객경험'을 무기로 내세운 것이다. (전자신문 발췌) 여기서 '고객경험'이란 무엇을 뜻하는 것일까? 고객경험이란 '고객이 원하는 기능과 제품. 그리고 고객의 삶을 편하게 만들어 준다고 느끼는 것'이라고 생각한다. 즉, 삼성과 LG는 단순히 TV가 아닌, 능동적인 디스플레이 자체로 삶의 일부가 되는 시장을 노리고 있다.

 삼성의 경우를 보자. 삼성전자는 독일 베를린에서 IFA 2022에서 브리핑을 가졌다. 급변하는 시장 환경에 맞게 고객경험을 포커싱했다. 포커싱의 요소는 다양한  TV서비스를 내세웠다. Work space(재택근무), Samsung Health(건강관리), Gaming Hub(게임), Live chat(실시간 채팅), 기본 업무, 교육, 취미 등 TV를 매개로 영위하는 능동적인 소비계층을 타겟으로 삼았다. TV는 더 이상 '화면을 보여주는 것'이 아니라, 라이프 자체가 된 느낌을 받는다.

한편, 가전제품에 발전을 이루는 것이, 마치 모바일 시장의 발전과 비슷한 모습을 보인다. 현재 삼성은 폴더블 폰을 앞세워 성장 모멘텀을 형성하고 있다. '갤럭시Z 폴드4', '갤럭시Z 플립4'등 새로운 폴더블 폰 시장에 집중하고 있다. 

 이어서 LG 같은 경우는, 원래 OLED(유기발광다이오드) TV로 시장에서 아주 높은 점유율을 갖고 있다. 놀랍게도, 여기서 멈추지 않고 '3초 전략'이라는 승부수를 띄웠다. '3초 전략'이란 초대형/초개인화/초경험 에 집중한다는 것이다. 압도적인 픽셀의 개수를 내세워 고화질로 생동감을 느끼게 할 수 있다. 

 이러한 삼성과 LG의 노력에도 불과하고, 반도체 시장이 잠시 둔화되었다는 건 부정할 수 없는 것 같다. 아무래도 코로나부터 시작해서, 우크라이나/러시아 전쟁, 지구온난화 등의 영향을 무시할 순 없다는 것이다. 또한(디스플레이와는 거리가 멀지만), 최근에 미국의 인플레이션 감축법(IRA) 때문에 전기차/배터리 시장이 흔들리고 있다. 이에 대해 한국이 어떤 조치를 취할지는 두고 봐야 할 것 같다.

그리고 무시할 수 없는 또 다른 사업체가 있는데, 바로 TCL, 하이얼 등과 같은 중국의 TV업체이다. 대륙의 실수라고 불리는 중국이지만, 시간이 점점 흐르면서 중국과 한국의 반도체 시장 차이는 점점 좁아지고 있다. 정말 비관적으로 본다면, 나중에는 'Made in China' 나 'Made in Korea'가 같은 급을 같게 된다면, 정말 슬플 것 같다. 그러기 전에, 내가 반도체 시장에 기여할 수 있다면..!  여튼, 중국의 진출을 염려하고 있는 삼성과 LG는 쉽게 카피하지 못하는 새로운 방식으로 사용자에게 접근할 것이라고 했다. 과연 그것이 무엇인지는 잘 모르겠다.

삼성과 LG가 이렇게 디스플레이 쪽에서 1,2위를 차지하고 있지만, 그 자리를 유지하는 게 정말 대단한 것 같다. 최근 삼성과 TSMC의 3 나노 경쟁에서 TSMC가 주 고객층(애플, 퀄컴, 앤비디아 등등)과 협력한 것을 보면 조금 아쉽긴 한데, 그래도 삼성은 GAA공정을 통해 경쟁력을 확보하는 것을 보면 또 어떻게 될지 모른다는 생각이 든다. 현재 삼성은 구글의 자체 칩 '3세대 텐서'에 3나노를 공급할 예정이라고 한다. 두 회사의 경쟁이 치열해지는 만큼, 소비자에겐 더 좋은 제품이 나오길 바란다!

더보기

컴활 실기 1급까지 D-14..!!

매일매일 기출 풀면서, 모르는 함수는 기록해서 기억하려고 노력하자.

그래서 오늘 볼 함수는 MATCH함수

MATCH 함수 설명

MATCH함수는 범위에서 일치하는 값이 아니라, 일치하는 값의 위치를 반환하는 함수이다. 

MATCH(찾을값, 범위, 옵션)

여기서 옵션에는 '-1', '0', '1' 세 가지 종류가 있다

MATCH(찾을값, 범위, -1) :

찾을값보다 크거나 같은 값 중 가장 작은 값을 찾는다. 범위는 반드시 내림차순으로 정렬되어 있어야 한다.

MATCH(찾을값, 범위, 0) :

찾을값과 정확하게 일치하는 값을 찾는다. 범위는 정렬되어 있지 않아도 된다.

MATCH(찾을값, 범위, 1) :

찾을값보다 크거나 같은 값 중에서 가장 큰 값을 찾는다. 범위는 반드시 오름차순으로 정렬되어 있어야 한다.

보통 옵션에서는 0이 자주 쓰이는데, -1과 1도 알아두면 좋다. MATCH함수의 예를 보며 마무리 하자.

MATCH(찾을값, 범위, 옵션) 예제

여기서 MATCH(100, $D$1:$D$16, 0) 를 넣으면, 값은 뭐가 나올까?

위에 보이다 싶이 3이 나온다. 여기서 알 수 있는 건, 같은 범위 내에 같은 숫자가 있더라도, MATCH함수는 가장 먼저 오는 값의 상대적 위치를 알려준다는 것이다.

MATCH함수는 INDEX와 많이 쓰이니까, INDEX함수도 공부하면 좋을듯 하다!

더보기

 

컴활 1급을 대학교 4학년이 되어서야 준비하는 나는.. 멍총이! 그래도 지금이라도 준비하지 않으면, 나중에는 더 큰 참사가 일어날 수 있다! 

오늘은 INDEX함수에 대해 알아보자

INDEX 함수

엑셀 공식 홈페이지에서는 " INDEX 함수는 테이블이나 범위에서 값 또는 값에 대한 참조를 반환하는 것"이라고 나와있다. 

즉, 함수의 테이블이나 범위에서 내가 원하는 행, 열 위치의 값을 반환하는 것이다.

INDEX함수의 예를 보면 쉽게 이해할 수 있다.

INDEX(범위, 행 번호, 열 번호)

셀 A13에 INDEX(A1:H11, 4, 4) 를 입력하면 값이 뭐가 나올까? 

당연스럽게도 A1:H11 범위의 4열, 4행의 값인 2018이 나오는 걸 볼 수 있다!

INDEX(범위, 행 번호, 열 번호)

아주 이지하게 INDEX 함수 클리어~!

다음에는 INDEX와 짝으로 많이 쓰이는 MATCH에 대한 얘기로 시작해야겠다.

컴활 1급 실기 원트에 합격 가즈아~

<Chrome 에드 블록을 사용한 PC에서 유튜브 광고 없이 보기>

상업적 광고 아님

불법프로그램 아님

글쓴이도 이렇게 해서 사용중

1. 크롬을 켜고 상단바의 가장 왼쪽에 보면 아래와 같이 <앱>이라는 것을 클릭해준다.

1-1. 만약 <앱>이 없다면 상단바에 우클릭 -> 북마크바 표시

2. 웹스토어 클릭

3. 웹스토어의 왼쪽 검색창에 '에드블록'을 검색 후 엔터

4. 가장 위에 있는 유튜브용 애드 블록 클릭

5. 오른쪽에 파란색 창에 'Chrome에서 설치'를 클릭

(저는 이미 설치해서 Chrome에서 삭제라고 표시되어 있습니다)

6. 설치해주고 크롬 껐다가 다시 켜고 유튜브에서 영상을 틀어서 확인

영상 우측 하단에 유튜브를 위한 애드블록에 의해 청소 Share가 뜨면 성공!

6-1 가끔씩 광고가 검은 화면으로 나올 때가 있는데, 한번 새로고침하면 그 이후로 없어짐

끝

여담.

유튜브에 광고를 게시할 수 있는 권리가 있듯이, 소비자는 광고를 보지 않을 권리가 있는 것입니다.

크롬측에서는 이 프로그램을 권장하지 않습니다.

그 이유는 주절주절 쓰여있는데, 결론적으로는 그냥 무시하시면 됩니다. 

유튜브 프리미엄 쓰지 마시고 이렇게 해서 광고 안보고 유튜브 영상 트시길..!!

정리에 앞서, 저는 현재 지거국 3학년으로 재학 중인 공대생입니다. 여기에 나와있는 내용들은 제가 직접 공부하고 요약해서 쓰기 때문에 정확하지 않은 정보가 있거나, 원하는 정보를 얻지 못하실 수 있습니다. 최대한 객관적이고 다양하게 준비해서 올리도록 노력하겠습니다. 자료의 출처나 내용에 대한 질문은 댓글이나 hcbeom9635@gmail.com으로 보내주시면 감사하겠습니다.

교재는 Steven C. Chapra, Applied Numerical Methods with MATLAB for Engineers and Scientists (4 th edition), McGraw-Hill, 2019의 재본판을 사용했습니다.

근(Roots)을 찾는 방법(Method)들

수치해석은 기본적으로 '해를 찾아가는 방법'들을 배우는 과목입니다. f(x) = 0 을 만족하는 x의 값을 해 또는 근 이라고 부릅니다. 우리가 수학을 배울 때는 일반적인 함수들 (ex 1차,2차,3차 함수)을 주로 다뤄서 상대적으로 해를 구하기가 쉬웠습니다. 하지만 더 복잡한 함수의 근을 구해야 할 때는 기존의 방법이 비효율적일 수 있습니다. 즉, f(x) = 0의 방정식으로 푸는 것이 아닌, 여러 과정을 통해서 근삿값을 구한 후, 점점 근에 점근하는 식으로 찾는 것입니다. 그것이 바로 수치해석의 목적입니다.

5장에서는 Bracketing Methods를, 6장에서는 Open Methods를 배웁니다. 앞선 글에서 말씀드렸지만, Bracketing Method와 Open Method는 각각 장단점이 있습니다. 그 내용은 아래 링크를 보시면 될 겁니다.

6장에서는 총 4가지 방법의 수치해법 과정을 배웁니다. 

1. Simple Fixed-Point Method

2. Newton-Rapshon Method

3. Secant Method (Modified Secant Method)

4. Brent's Method -> Bracketing Method + Open Method

이번 장에서는 Simple Fixed-Point Method만 알아보겠습니다.

Simple Fixed-Point Method란?

x=g(x)의 함수 형태를 사용하여 근을 찾아내는 수치해법이다. 

하나의 예시를 들어서 설명해보겠다.

f(x)의 형태가 주어질 때 x=g(x)의 형태로 변환한다. 그러면 f(x)=g(x)라는 방정식이 나오게 되고, 두 그래프의 교점의 x좌표가 근이 되는 것이다.

또한 Bracketing Method와는 다르게 구간이 필요없어서 적당한 초기값을 설정해서 근을 구하면 된다.

예시는 초기값을 0으로 두고 풀었을 경우이다.

또한 근사 오차와 참 상대 오차도 구했다. 

여기서 좀 더 자세히 보면, 참 오차가 계속 비슷한 비율로 줄어드는 것을 볼 수 있습니다.

그 이유는 평균값 정리와 관계가 있습니다.

마지막으로 Open Method는 발산하는 단점이 있다고 했는데, Simple Fixed-Point Method에서 발산하는 경우를 알아보겠습니다. 첫 초기값인 X0에 대해서 도함수의 절댓값이 1보다 크면 발산하는 경향이 있습니다. 아래의 예시를 보면 더 와닫을 것입니다.

정리에 앞서, 저는 현재 지거국 3학년으로 재학 중인 공대생입니다. 여기에 나와있는 내용들은 제가 직접 공부하고 요약해서 쓰기 때문에 정확하지 않은 정보가 있거나, 원하는 정보를 얻지 못하실 수 있습니다. 최대한 객관적이고 다양하게 준비해서 올리도록 노력하겠습니다. 자료의 출처나 내용에 대한 질문은 댓글이나 hcbeom9635@gmail.com으로 보내주시면 감사하겠습니다.

교재는 Steven C. Chapra, Applied Numerical Methods with MATLAB for Engineers and Scientists (4 th edition), McGraw-Hill, 2019의 재본판을 사용했습니다.

근(Roots)을 찾는 방법(Method)들

수치해석은 기본적으로 '해를 찾아가는 방법'들을 배우는 과목입니다. f(x) = 0 을 만족하는 x의 값을 해 또는 근 이라고 부릅니다. 우리가 수학을 배울 때는 일반적인 함수들 (ex 1차,2차,3차 함수)을 주로 다뤄서 상대적으로 해를 구하기가 쉬웠습니다. 하지만 더 복잡한 함수의 근을 구해야 할 때는 기존의 방법이 비효율적일 수 있습니다. 즉, f(x) = 0의 방정식으로 푸는 것이 아닌, 여러 과정을 통해서 근삿값을 구한 후, 점점 근에 점근하는 식으로 찾는 것입니다. 그것이 바로 수치해석의 목적입니다.

5장에서는 Bracketing Methods, 6장에서는 Open Method를 배우고, Bracketing Methods + Open Methods = Brent's Methods도 뒤에 나옵니다. 

우선 5장의 Bracketing Methods를 알아보겠습니다.

Bracketing Methods

Bracketing Methods는 구간을 정하고 근을 추정하는 방법입니다. 그렇기에 구간을 위한 2개의 초기값을 요구합니다.

장점은 정확하게 근을 추정할 수 있다는 것이고,

단점은 속도가 느리다는 것입니다.

뒤에서 배우겠지만 Open Methods는 반대로 속도가 빠르지만, 정확하지 않아서 발산할 가능성이 있습니다.

Bracketing Methods에는 Bisection Method와 False position Method가 있습니다.

• 근을 추정하는 구간을 정했을 때 나타는 여러 경우들

• (a), (b) 경우

• (c), (d) 경우

• 일반적으로 두 경계치 간의 함수값의 곱이 양수이면 근이 존재하지 않고, 함수값의 곱이 음수이면 근이 존재한다. 그러나 (e), (f)의 경우처럼 두 경계치의 값이 양수임에도 근이 존재할 수 있고, 음수여도 근이 존재하지 않거나 중근이 존재할 수 있다. 즉, 여러 경우에 대해 정확한 알고리즘 개발은 매우 힘든일이다. 그래서 수치해법을 사용해야 하는 것이다.

• Bracketing Method에서는 주로 두 경계치를 알맞게 정했다는 가정하에 시작하므로, 두 경계치의 곱을 통해서 근을 찾아낼 수 있다. 그 방법을 Incremental search라고 한다.

(1). Bisection Methods

• absolute error는 bisection method에서 나타나는 에러이다. 이것을 통해 원하는 횟수 n을 구할 수 있으며, 반대로 원하는 횟수 n번에 대한 에러를 찾아낼 수도 있다.

(2). False Position

근을 쉽게 찾기 위해 경계의 함수크기를 고려한다. 주로 Bisection보다 효과적이고, 오차가 빨리 감소하는 장점이 있다.

항상 bisection보다 좋은 것은 아닌데, 이렇게 심한곡률을 가진 함수는 너무 느리게 수렴하는 단점이 존재한다.

정리에 앞서, 저는 현재 지거국 3학년으로 재학 중인 공대생입니다. 여기에 나와있는 내용들은 제가 직접 공부하고 요약해서 쓰기 때문에 정확하지 않은 정보가 있거나, 원하는 정보를 얻지 못하실 수 있습니다. 최대한 객관적이고 다양하게 준비해서 올리도록 노력하겠습니다. 자료의 출처나 내용에 대한 질문은 댓글이나 hcbeom9635@gmail.com으로 보내주시면 감사하겠습니다.

저는 공부할 때 Discrete Mathematics - Richard Johnsonbaugh 7th 제본판을 사용했습니다.

이산수학 1장. Sets and Logic

연산자(Quantifier)

이산수학 1장에서는 두 가지의 연산자를 배웁니다.

Universal Quantifier ∀

Existential Quantifier ∃

입니다.

• Universal Quantifier  ∀xP(x)

"for every" , "for all" 즉, 모든 x에 대해 만족하는 명제를 나타낼 때 쓰입니다. Universal Quantifier 명제가 참인지 거짓인지 판별하기 위해서는 반례(CounterExample)를 들어서 판별할 수 있습니다. 모든 x에 대해 만족하는 명제가 거짓이라면, 그 명제를 만족하지 않는 x를 찾으면 됩니다. 수식으로 설명해보겠습니다.

Ex)

• Existential Quantifier  ∃

"there exist" 즉, 명제에 해당하는 x의 값이 하나라도 '존재'하는지의 여부를 확인할 때 쓰입니다. 예시를 통해 확인해보겠습니다.

Ex)

그렇다면 이 두 가지를 동시에 쓸 수는 없을까요? 당연히 쓸 수 있습니다. 그런 경우를 Nested Quantifier라고 합니다.

• Nested Quantifier

Ex)

모든 x에 대해 식을 만족하는 모든 y가 있다면 명제는 참입니다. Nested Quantifier에 드모르간 법칙을 사용하면 아래와 같이 됩니다.

드모르간 법칙을 사용할 때 주의할 점은, ∀이 not을 취하면 ∃이 되고, ∃이 not을 취하면 ∀가 되는 것이 핵심입니다. 또한 명제에도 Not을 포함해줘야 합니다.

정리에 앞서, 저는 현재 지거국 3학년으로 재학 중인 공대생입니다. 여기에 나와있는 내용들은 제가 직접 공부하고 요약해서 쓰기 때문에 정확하지 않은 정보가 있거나, 원하는 정보를 얻지 못하실 수 있습니다. 최대한 객관적이고 다양하게 준비해서 올리도록 노력하겠습니다. 자료의 출처나 내용에 대한 질문은 댓글이나 hcbeom9635@gmail.com으로 보내주시면 감사하겠습니다.

저는 공부할 때 Discrete Mathematics - Richard Johnsonbaugh 7th 제본판을 사용했습니다.

이산수학 1장. Sets and Logic

명제란?

명제(Proposition)이란 참인지 거짓인지 결정할 수 있는 문장을 뜻합니다. 우리는 일상 속에서 수많은 대화를 주고받습니다. 그 말 중에서는 명제인 것도 있고 아닌 것도 있습니다. 예를 들어서 확인해보겠습니다.

ex)

1) 7을 나눌 수 있는 양의 정수는 오직 2와 5이다. -> 거짓으로 판단되므로 명제가 맞다.

2) 모든 양의 정수 n에 대해, n 보다 큰 소수(prime number)가 있다. -> 참으로 판단되므로 명제가 맞다.

3) x + 10 = 14 -> x의 값에 따라 참 또는 거짓이 될 수 있으므로 명제가 아니다. 즉, 참인지 거짓인지 판명 불가.

• p 와 q 가 명제 일 때,
• conjunction (AND) : p ∧ q
  disjunction (Inclusive-OR) : p v q
  disjunction (Exclusive-OR) : p v q
  negation (NOT) : ~ p , ¬ p

Truth Table

명제는 다양한 연산자를 갖고 있는데, 이 연산자에는 '연산우선순위'가 존재합니다. 어려울 것 없습니다. 괄호가 없을 때 연산자 우선순위는 (not) -> (and) -> (or)의 순으로 연산하면 됩니다.

Conditional Proposition(조건 명제)

조건 명제에 대해 알아보겠습니다. 흔히 얘기하는 "p 이면 q 이다"라는 것이 조건 명제입니다. p는 가정이며, q 는 결론에 해당합니다. 이것을 수식으로 써서 표현하면 p -> q 가 됩니다. 그리고 또 한 가지, 영어로 표현하면 "if p, then q" 또는 "p only if q"인 경우도 모두 p->q와 같은 의미로 받아들이면 됩니다. 

어떤 명제의 진리값이 같다면 명제 P와 Q는 logically equivalent하다고 하고, 수식으로는 방정식의 '='처럼 세 줄로 나타냅니다.

• Biconditional Propositions

바이컨디셔널 프로포지션은 한국말로 '필요충분조건' 입니다. 어렵게 왜 영어로 썼냐구요? 대학가면 다 그렇답니다...

여튼 필요충분조건은 문제에서 " p if and only if q"라고 많이 씁니다. 논리식과 여기표는 다음과 같습니다.

• 역(Converse) & 대우(Contrapositive)

역과 대우는 아주 중요한 개념입니다. 주어진 명제가 참인지 거짓인지 판별할 때 역이나 대우를 이용하며 증명하는 경우도 있으니까요..! 역과 대우의 여기표는 다음과 같습니다.

• Arguments

Deductive reasoning(연역적 추론) : 연속적인 명제들로부터 결론을 도출하는 과정

여기서 Argument는 가정들이 모두 참일 경우에 결론이 참이라는 것을 말합니다. 만약 가정에서 거짓이 존재한다면 결론은 거짓입니다. 수식으로 살펴보겠습니다.

• Rules of Inference (추론의 규칙)

이산수학을 배웠다면 여기 부분에서 가장 골머리가 아플 것이다. 그러나 차근차근 공부하다보면 알게된다. 여기 부분은 나중에 더 자세하게 써야겠다... 일단 외워!

정리에 앞서, 저는 현재 지거국 3학년으로 재학 중인 공대생입니다. 여기에 나와있는 내용들은 제가 직접 공부하고 요약해서 쓰기 때문에 정확하지 않은 정보가 있거나, 원하는 정보를 얻지 못하실 수 있습니다. 최대한 객관적이고 다양하게 준비해서 올리도록 노력하겠습니다. 자료의 출처나 내용에 대한 질문은 댓글이나 hcbeom9635@gmail.com으로 보내주시면 감사하겠습니다.

저는 공부할 때 Discrete Mathematics - Richard Johnsonbaugh 7th 제본판을 사용했습니다.

이산수학 1장. Sets and Logic

집합(Set)이란?

Set(집합)은 서로 다른 물체들의 모음 입니다. 그리고 집합 안에 있는 것을 Elements(원소)라고 불립니다.

예를 들어 집합 A에 원소 x가 있다면 아래와 같이 간단하게 표현합니다.

x라는 원소를 조금 더 구체화 시켜서 예를 들어봅시다.

A안에 {1,3,5,7}라는 원소가 있어서 1은 A에 속한다고 볼 수 있습니다. 

또한 B안에는 k가 0~5까지의 상수이므로 {1,3,5,7,9,11}라는 원소가 있어서 3또한 A에 속합니다.

이렇게 간단하고 유한한 집합을 Finite sets이라고 불립니다.

반대로 무한한 집합을 Infinite sets이라고 합니다. 무한한 집합은 무엇이 있을까요? 대표적인 예만 들어보자면

정수의 집합은 무한한 집합입니다.

이렇듯 사용자에 따라 여러 가지 종류의 집합을 만들 수 있습니다. X, Y라는 집합이 있을 때, X의 모든 원소가 Y에 포함된다면 X는 Y의 부분집합(subset)이며 기호로는 아래처럼 나타낼 수 있습니다.

또한 X가 Y의 부분집합일 때 X≠Y이면 X는 Y의 진부분집합(proper subset)라고 하며 기호로는 다음과 같습니다.

여기서 중요한 점은, 대부분 교육과정에서는 부분집합과 진부분집합의 표기를 혼용해서 사용하는 것입니다. 사실 중요한 부분은 아니므로 그냥 넘어가도 좋습니다. 만약 교수님께서 구분해서 사용하신다면 그렇게 쓰고, 아니면 아닌 대로 쓰면 됩니다..하하

예를 들어 아래와 같은 집합 A,B가 있으면 A는 B의 부분집합으로 볼 수 있습니다.

생소한 집합인 멱집합(Power Set)와 기수(Cardinality)라는 것을 알아보겠습니다.

멱집합은 집합 X의 모든 부분 집합의 집합입니다.

직관적으로 알 수 있도록 식으로 보면 아래와 같습니다.

기수(Cardinality)는 집합 안의 원소의 수를 뜻합니다. 기호로는 절댓값처럼(A의 기수 = |A|) 쓰면 됩니다.

집합 A에는 a,b의 두 가지 원소만 있으므로

여기서 멱집합과 기수간의 관계를 알아보겠습니다. 

A = {a, b} 이고 P(A) = {∅, {a}, {b}, {a,b}}이므로 |P(A)| = 4 

즉, 집합 A의 원소가 n개일 때 멱집합A의 기수는

집합 안에는 또 다른 집합이 있는 경우도 있습니다. 그런 경우를 벤다이어그램으로 나타내면 아래와 같고, 이러한 모음을 Pairwise Disjoint라고 합니다.

Partition이라는 것은 X가 nonempty subsets S의 모음일 때, X안의 모든 원소들이 S의 한 멤버 안에만 속해 있다면 S는 X의 partition이라고 합니다. 즉, S가 X의 partition이면 S는 pairwise disjoint하다고 볼 수 있습니다.

글로만 보면 확 와닿지 않는데, 예시를 보면 쉽게 이해할 수 있습니다.

마지막으로 Cartesian Product(데카르트 곱)에 대해서 알아보겠습니다. 데카르트 곱은 기호로 X x Y이며 정의는

x ∈ X and y ∈ Y 인 모든 순서쌍 (x,y)들의 집합이다. 데카르트 곱의 예시를 보고 이해해보겠습니다.

지금까지 집합에 대한 내용을 알아봤습니다. 사실 집합은 중학생 때부터 배운 것들이라서 이해하는데 큰 어려움이 없습니다. 그러나 생소한 용어와 영어로 나오니까 몰랐던 부분은 체크하는 게 좋습니다. 다음장에서는 명제를 알아보겠습니다.